MLP for Fashion MNIST Classification
Introduction
In this project, we implement a Multilayer Perceptron (MLP) neural network with weight decay regularization to solve the Fashion MNIST classification problem. The Fashion MNIST dataset contains grayscale images of various fashion items categorized into ten classes. The goal is to train a neural network to classify these fashion items accurately.
Dataset and Preprocessing
The Fashion MNIST dataset is utilized, divided into three sets: training, validation, and test. Each image within the dataset is a 28×28 grayscale image, with pixel values being scaled between 0 and 1 by dividing them by 255. Furthermore, the target labels are converted into a one-hot encoded format.
Neural Network Architecture
MLP Architecture
The MLP architecture that has been implemented comprises multiple fully connected (dense) layers. The architecture is as follows:
- Input layer: 784 units (representing the flattened 28×28 image)
- Hidden layers: Three hidden layers, each consisting of 32 units
- Output layer: 10 units (corresponding to the ten fashion classes)
Activation Function
The Exponential Linear Unit (ELU) activation function is employed for all layers except the output layer. ELU is defined as follows:
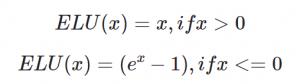
This activation function serves to mitigate the vanishing gradient problem.
Softmax Activation
The Softmax activation function is utilized in the output layer to compute class probabilities.
Training
Loss Function
The Softmax Cross-Entropy loss function is used to gauge the disparity between predicted and actual class probabilities. To tackle overfitting, weight decay regularization is employed.
Optimization
A batch size of 32 is employed, and the model is trained using mini-batch stochastic gradient descent (SGD) with a learning rate of 0.01. Throughout the training process, the model parameters (weights and biases) are updated based on computed gradients.
Hyperparameter Tuning
Hyperparameter tuning is performed by conducting experiments with different learning rates (0.01 and 0.05) and regularization strengths (0.01, 0.03, and 0.05). The selection of the best-performing model is determined by validation set performance.
